A Marangoni tractor beam for droplets
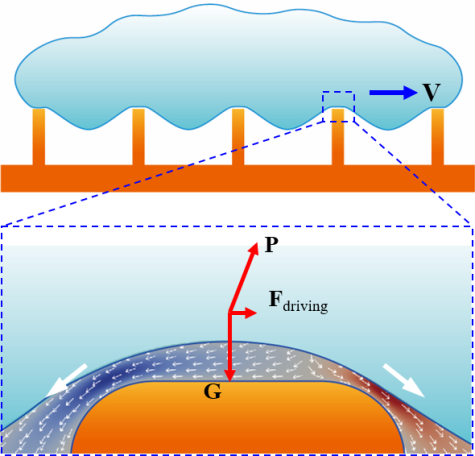
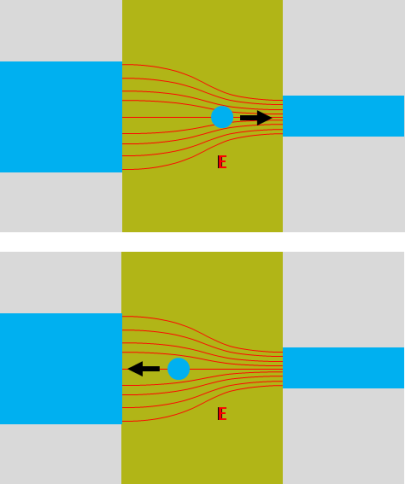
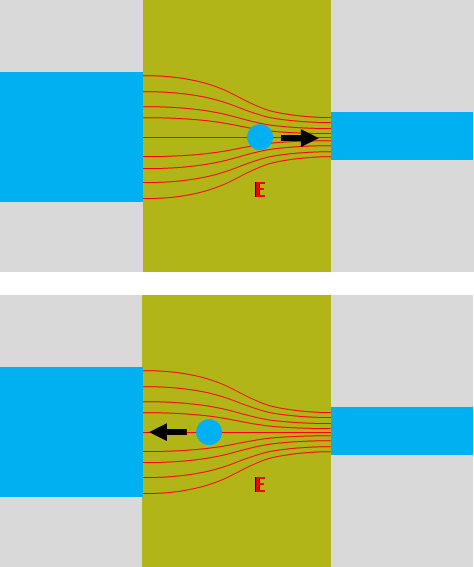
In a team with colleagues from the University of Twente we uncovered the counter-intuitive motion of small oil droplets in a channel flow. The liquid inside the channel is water, with a jet of alcohol in the center that flows around a droplet. Due to diffusion, the flow direction and the geometric arrangement, the alcohol content varies along the droplet surface. This in turn creates a surface tension difference between the top and the bottom of the droplet that results in a so-called Marangoni force pulling the droplet in the upstream direction. Applications where this effect could be leveraged range from large scale emulsion or bubble systems in process engineering to analytical chemistry for the collection and handling of small liquid samples. The work was published in the journal Soft Matter and will be featured on the front cover.
Spontaneous symmetry breaking as a motor for Leidenfrost drops
Almost everyone is familiar with the Leidenfrost effect: a drop of water on a hotplate does not touch the surface, but is held at a distance by a thin film of steam, which gives the drop a high degree of mobility. However, the movement of the drop on the hotplate is undirected and erratic. About two decades ago, it was discovered that a Leidenfrost drop moves in a directional and controlled manner on a surface with the structure of a ratchet. The reason is that the asymmetry of the ratchet ensures that the vapor below the drop escapes in a preferred direction, which propels the drop. In a co-operation with Cunjing Lv and his group, a professor at Tsinghua University in China and a former postdoc of our group, we found a similar drop motion on completely symmetric surface structures, e.g., on metal surfaces with parallel grooves. Our theoretical model explains this effect: Once set in motion, the liquid surface near the hot metal surface is asymmetrically deformed and thus provides the permanent drive for the drop. In this case, it is not the solid surface but the liquid surface that forms the ratchet. The results were published in the journal Science Advances. In a more general context, this phenomenon is known as spontaneous symmetry breaking: An initially symmetric system dynamically evolves into a state in which the symmetry is broken. The principle is so general that the findings from the experiments with Leidenfrost drop could be used to develop new concepts for transporting liquids on the millimeter or micrometer scale.
Vibrations reduce the surface tension of liquids
If a liquid volume is vibrated with sufficient amplitude, capillary waves emerge on its surface, termed Faraday waves. With increasing excitation amplitude, these waves become more and more chaotic. Interestingly, a liquid volume with chaotic Faraday waves behaves as if it has a reduced surface tension, which we have shown using a combination of experiments and theoretical models. In this way, we have been able to map a complex time-dependent system to a much simpler system, i.e., a steady-state capillary surface. This work was recently published in Physical Review Letters and has been highlighted on the homepage of TU Darmstadt.
Incompressible surfactants on the move
Even relatively small amounts of surfactants, molecules that attach to the interface between two fluids, can behave nearly incompressible at the interface. For liquid flowing over an elongated rectangular gas-filled cavity embedded in a planar wall, this incompressibility may render the interface immobile as long as the interface remains planar. By adjusting the gas-pressure in the cavity, the gas-liquid interface can be deflected above or below the planar wall. We find that in this case liquid flowing over the cavity sets the interface in motion, inducing a recirculating flow pattern at the interface.
Baier, Hardt, Shear flow over a surface containing a groove covered by an incompressible surfactant phase, J. Fluid Mech., 949, A34 (2022), https://doi.org/10.1017/jfm.2022.775
Tuning the wavelength of electrically induced waves
When a time-varying electric field acts on the interface between two immiscible liquids, characteristic waves form at the interface. A similar thing happens when two superposed liquids are vibrated using a shaker. These interface waves form in a self-organization process, and up to now, it was unknown how to tune their wavelength. We have found a way to exactly do that, as we show in a recently published paper: We superpose the time-varying field that drives the waves with a constant field. The results nicely agree with the predictions of a theoretical model we have developed.
Electrically-induced Faraday waves
It is well-known that wave patterns (so-called Faraday waves) emerge on a vibrated liquid film. Not only mechanical forces can induce such wave patterns, but also electric forces, for example when keeping the liquid in a parallel-plate capacitor to which an AC voltage is applied. Remarkably, electrically induced Faraday waves have hardly been studied experimentally, although electric forcing offers options to control the wave patterns not available with mechanical forcing. We have studied the wave patterns of the electrically induced Faraday instability for the first time and compared them to theoretical predictions accounting for viscosity effects, with the result that there is a good agreement between experiments and theory.
From Taylor cones to surface dimples
It is well known that fluid interfaces disintegrate under sufficiently strong electric fields, leading to electrohydrodynamic tip streaming, often in form of a Taylor cone. However, when we studied the influence of a local electric field on an oil-water interface, an alternative deformation mode emerged: Here, the interface is pushed away from the electrode, and additional cone structures form at the rim of the dimple. Using experimental and numerical methods, we show that small droplets inside the oil phase play a crucial role in the dimple formation. They induce a background flow, which in turn perturbs the interface.
Partial droplet coalescence – where does it end?
When an electric field derives a water droplet to an interface between oil and water, under certain circumstances partial coalescence is observed. This means that instead of merging with the water volume, the droplet bounces back, whereupon it looses a part of its volume. The product droplet can again be driven to the oil-water interface, and the whole process can be repeated, resulting in sucessively smaller droplets. We have performed corresponding experiments with a large number of successive partial-coalescence events and could produce droplets with diameters of about 400 nm. The fact that we could not observe any smaller droplets is probably due to the optical resolution limits of our microscope. Would this process still work for droplet diameters of a few nanometers?
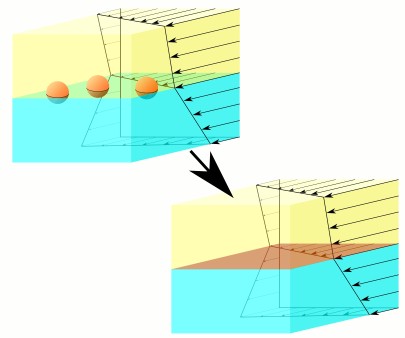
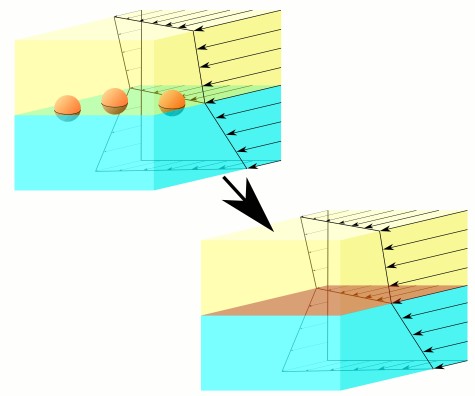
Fluid interfaces can become solid-like
As a stream encounters an obstacle, floating debris sometimes piles up in front of the obstacle, forming a dense layer on the water surface. At a microscopic scale, surfactants, molecules attached to the interface between two fluids, can suffer the same fate, immobilizing the interface upstream of an obstacle. ‘Super-hydrophobic’ surfaces with embedded gas pockets have been suggested for reducing drag on objects moving through water. With this in mind, we investigated the impact that surfactants have on this mechanism and found that parts of the gas-water interface become ‘solidified’ by surfactant pile-up.
Also fluid interfaces can be viscous
Usually, viscosity is a quantity associated with the bulk of a fluid. If, however, small particles or surfactants are adsorbed to a gas-liquid or liquid-liquid interface, the interface itself becomes viscous. In that case, the viscosity coefficients represent the dissipation due to the presence of particles or surfactants in an average manner. We have recently derived analytical expressions for the viscosity coefficients of a particle-laden fluid interface in the limit of low particle concentrations. These results could significantly simplify simulations of two-phase flows with particle-laden interfaces.
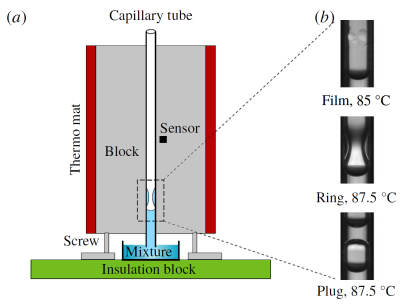
“Tears of wine” in capillary tubes
“Tears of wine” is a phenomenon that can be observed in wine glasses: Driven by Marangoni stresses, a liquid film crawls up along the glass wall. Now imaging shrinking the diameter of the wine glass to one millimeter. In that case, ring-like structures are formed from the film. These liquid rings finally collapse and form plugs that are propelled along the capillary tube by evaporation. We have studied this phenomenon based on experiments and theory.
Species transfer using small droplets as carriers
Transferring chemical species or nanoparticles in a controlled way becomes challenging when very small species amounts are considered. We have found a solution to this problem, where a droplet with a diameter of the order of 5 µm serves as carrier for the cargo. The method is sketched in the schematic on the left. The droplet reciprocates between two aqueous reservoirs under the influence of a DC electric field. Upon touching the reservoir, the droplet reverses its charge and its direction of motion. We have studied the transfer of chemical species between the two reservoirs mediated by the droplet.
Non-contact electrostatic manipulation of droplets on liquid-infused surfaces
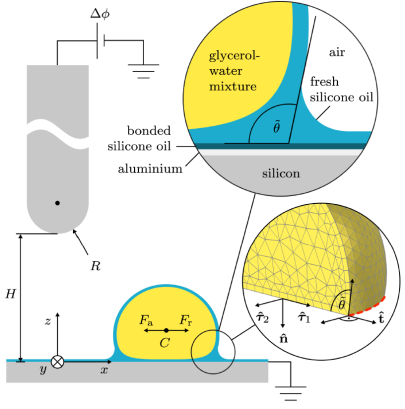
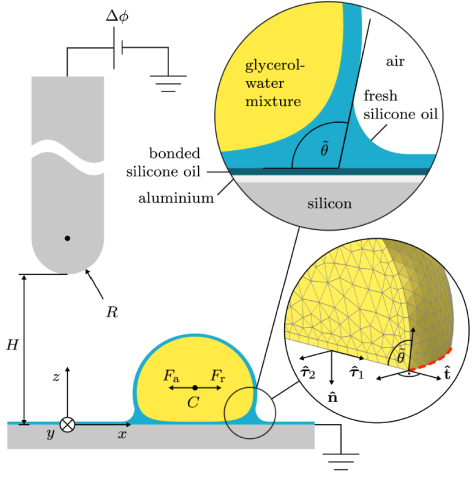
Liquid-infused surfaces have unique liquid-repelling properties. In comparison with conventional superhydrophobic surfaces, liquid-infused surfaces provide stable wetting states and pronounced self-healing properties. We have established the manipulation of highly mobile droplets sitting on silicone-oil infused surfaces by exploiting a non-uniform electric field between a grounded substrate and a non-touching pin electrode placed above it. Droplets are attracted towards the pin electrode, and translational velocities can exceed 1 cm/s.
On-demand production of femtoliter droplets in microchannels
We have developed a method to produce monodisperse droplets inside microchannels with volumes in the femtoliter range on demand. The method utilizes pulsed electric fields deforming the interface between an aqueous and an oil phase and pinching off droplets. It can be applied even to solutions with a zero-shear rate viscosity more than ten thousand-fold higher than that of water. The droplets may serve as biological reaction compartments.
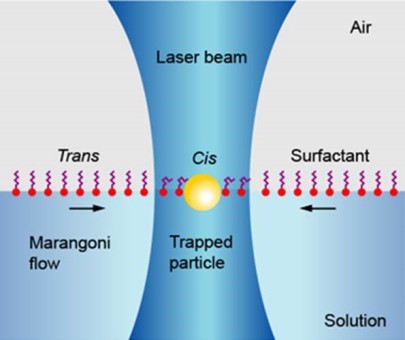
Controlling the trajectories of nano/micro particles using light-actuated Marangoni flow
The ability to manipulate small objects and to produce patterns on the nano- and microscale is of great importance, both with respect to fundamentals and technological applications. The manipulation of particles with diameters of the order of 100 nm or below is a challenge because of their Brownian motion but also because of the scaling behavior of methods such as optical trapping. We have developed a method enabling the trapping and manipulation of nano- and microparticles based on interfacial flows controlled by visible light. The inherent advantages of this method are the linear scaling of the trapping force with the particle diameter and the fact that the force is less dependent on particle properties than in the case of conventional methods.
Electrophoresis of surface particles
The electrophoresis of particles immersed in a liquid is a well-studied phenomenon. However, what happens when a particle attached to a liquid surface translates along that surface driven by an electric field has been largely unknown. We have computed the electrophoretic mobility of a particle at the interface between two fluids with large viscosity contrast. For thin Debye layers, the Smoluchowki mobility is recovered. Generally, the mobility depends on the contact angle between the fluids and the particle. We have also calculated the interfacial deformation caused by the Debye layer around the particle.
Stability of holes in liquid films
If you spill liquid over a surface, it forms a film with a thickness of the order of its capillary length. If the surface is bounded and you did not spill enough liquid, a hole will form. The stability of the hole depends on its size. There is a threshold size below which it collapses. For a water film, the collapse is dominated by inertia. We studied the stability and collapse of holes in liquid films in detail and compared the experimental results with mathematical models and simulations.
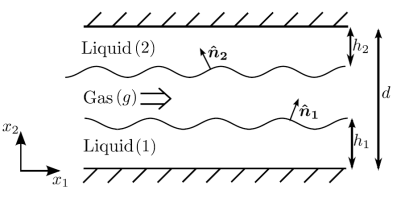
Instabilities in microchannel gas-liquid flows
In a parallel-plates microchannel where the walls are coated with liquid films, separated by a gas layer in the middle, the gas flow triggers characteristic instabilities of the films. Interestingly, the instability patterns become synchronized between the two films, i.e. the upper film “knows” what the lower film does. For example, in many cases the mirror-symmetric mode (with respect to x2, see the figure) dominates. We have performed a detailed analysis of the coupled instability modes.
Individual droplet size control in a microfluidic T-junction droplet generator
Electric fields can be used to control the size of individual aqueous droplets produced at a microfluidic T-junction. Under a sufficiently strong electric field, the droplet diameter is about half of the diameter obtained without electric field. Using electric field pulses with a duration of the order of the inverse droplet production frequency, the size control of individual droplets produced in a continuous stream becomes possible. Based on that, arbitrary droplet size sequences can be encoded.
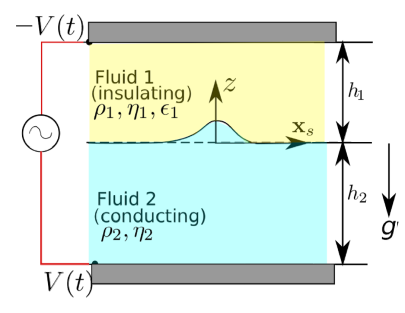
Excitation of fluid interfaces with AC electric fields
An interface between a dielectric and a conducting fluid can be excited using an AC electric field. When the electric field strength exceeds a threshold voltage, patterns with a characteristic wavelength appear at the fluid interface. Different from the Faraday instability, a related case where the interface becomes unstable due to a periodic acceleration, the response of the system is very complex when excited by a superposition of different frequencies. We have analyzed the instability modes using Floquet theory. Corresponding instabilities may be utilized for pattern formation based on self-organization.
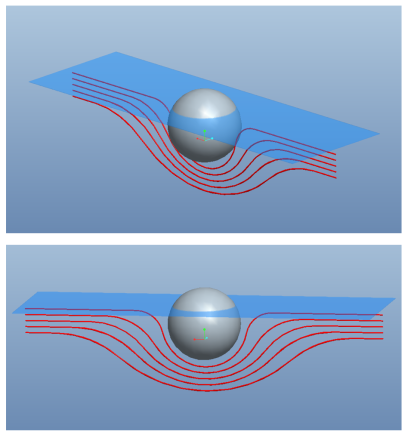
Stokes drag on a sphere translating along a fluid-fluid interface
Presumably the most well-known achievement of George Gabriel Stokes is his formula for the drag force experienced by a sphere translating in an unbounded fluid at low Reynolds numbers. However, in some scenarios small particles are attached to an interface between two immiscible fluids, constrained to tangential motion relative to the interface. We have analyzed this situation and derived a generalization of Stokes’ law for large viscosity contrast and small capillary number. The image at the left is a sketch of the corresponding streamlines.
Structuring thin liquid films utilizing the Bénard-Marangoni instability
If a system of two superposed liquid films is exposed to a temperature gradient normal to the films, the upper layer exhibits convection cells which deform the lower thin film in an identical pattern. This effect can be seen in the figure above, which displays the hexagonal convection cells and the humps of the thin film below. The principle could find applications in fabricating regular, highly ordered surface structures.